Praca dla detektywa: jak sprawdzić dlaczego Ziemia się ociepla?

Praca naukowca przypomina pracę detektywa – obie polegają na szukaniu wskazówek i wysnuwaniu wniosków. Sprawdź, jak to się robi! O naukowym rozumowaniu, logicznym dowodzeniu hipotez i swoich doświadczeniach z prowadzenia wykładów opowiada Marcin Popkiewicz.

Jak pokazało opublikowane w 2025 r. badanie Eurobarometru dotyczące wiedzy naukowej Europejczyków, ponad połowa Polaków nie wierzy w antropogeniczne przyczyny obecnej zmiany klimatu. To poniekąd rozbrajające, bo to kwestia z zakresu nauki i decyduje tu nie wiara lecz wiedza. Zastanówmy się więc, jak taką wiedzę zdobyć i jak w ogóle zdobywamy wiedzę. Zanim przejdziemy do działania ziemskiego systemu klimatycznego i obserwacji, spróbujmy zrozumieć podstawy rozumowania naukowego i tego, jak działa nauka – na dwóch prostych przykładach i prostym językiem.

Akt 1. Moneta spadająca na podłogę

Podczas wykładu wyjmuję z kieszeni monetę, taką zwykłą pięciozłotówkę:

Trzymam ją przed sobą i pytam się zebranych: “za chwilę tę monetę puszczę… jak myślicie: czy uniesie się pod sufit, podryfuje w powietrzu w Waszą stronę czy spadnie na podłogę”?

Słuchacze patrzą na mnie podejrzliwie, z myślą, że musi być w tym jakiś haczyk, ale mówią, że „jasne, że spadnie”. Puszczam monetę, a ta… faktycznie spada.

Dla wszystkich było oczywiste, że tak się stanie, bo wiemy, że prawo grawitacji działa.

Drugie pytanie, które zadaję jest już trudniejsze: “Po jakim czasie moneta spadnie na podłogę? Trzymam ją na wysokości… (tu wyjmuję miarkę i odmierzam wysokość nad podłogą) 125 cm. Kto wie, jak to policzyć i wie jakiego wzoru użyć?”

Gdy w wykładzie uczestniczą normalni ludzie, dość rzadko trafia się osoba, która potrafi podać właściwą odpowiedź; choć to poziom fizyki ze szkoły średniej. Typowe odpowiedzi, które słyszę brzmią „ułamek sekundy” czy „niecała sekunda”.

Jednak nawet jeśli słuchacze akurat nie wiedzą ktoś nie wie, jak przeprowadzić odpowiednie obliczenia, to są ludzie, którzy to potrafią. Wzór pozwalający obliczyć czas t spadku ciała z danej wysokości h wygląda:

$t=\sqrt{2h \over g}$

gdzie g to przyspieszenie ziemskie, a wszystkie wielkości wyrażamy w jednostkach układu SI, czyli czas w sekundach, wysokość w metrach itd.

Po podstawieniu h = 1,25 m oraz g = 9,81 m/s² ≈ 10 m/s² otrzymujemy czas spadku

$t=\sqrt{{2 \cdot 1,25} \over 10}=\sqrt{1,5 \over 10}=\sqrt{1 \over 4}={1 \over 2} = 0,5 s$

Wysokość 1,25 m jak widać jest nieprzypadkowo tak dobrana, że wychodzi czas spadku równy pół sekundy.

Może nie każdy na sali wiedział jaki wzór zastosować, ale mamy doświadczenie ze spadającymi rzeczami i wiemy, że moneta z tej wysokości ani nie spadnie w milisekundę, ani nie będzie spadać przez minutę.

Ale… czy rachunek aby na pewno jest poprawny? Czy moneta faktycznie będzie spadać dokładnie pół sekundy? To trzecie pytanie do osób na sali.

Po chwili zastanowienia padają różne odpowiedzi, np.:

• przyspieszenie ziemskie zostało zaokrąglone do 10 m/s²;
• moneta mogła spaść pionowo lub na płask – w tym pierwszym przypadku krawędź monety dotknie podłogi wcześniej niż w drugim;
• wysokość 125 cm nad podłogą mogłem zmierzyć niedokładnie (i czy mamy na myśli jej środek ciężkości czy dół?);
• moja dłoń w momencie puszczania monety mogła nie być idealnie nieruchoma, lecz lekko przemieszczać się w górę lub w dół, co wpływa na czas spadku;
• jeśli na podłodze jest miękka wykładzina dywanowa sama definicja momentu upadku nie jest wcale łatwa do określenia;
• obliczenia nie uwzględniają tarcia powietrza;
• nie uwzględniłem efektów relatywistycznych i lepsze obliczenia od wzorów wynikających z teorii grawitacji Newtona dałaby ogólna teoria względności Einsteina;
• …i wiele innych

Czy wszystko to oznacza, że skoro tego wszystkiego nie uwzględniliśmy, to nasze oszacowanie jest bezużyteczne? Absolutnie nie – moneta tak czy inaczej będzie spadać pół sekundy, może 0,01-0,02 sekundy mniej lub więcej – co z punktu widzenia interesującej nas w życiu codziennym dokładności nie na żadnego znaczenia. Ale jak ktoś chciałby zasiać wątpliwości odnośnie naszej umiejętności przewidzenia czasu spadku monety, to miałby się czego czepiać i twierdzić, że nasz wzór jest do kitu.

Czas na czwarte pytanie do osób na sali: przychodzi ktoś, kto mówi, że zastosowany wcześniej wzór jest niewłaściwy, a zamiast tego do obliczenia czasu spadku monety t z wysokości h należy użyć zależności:

$t={1 \over 2} h$

Wynikający z niego czas spadku monety z wysokości 1,25 m to 0,625 s. Konia z rzędem temu, kto na oko potrafi wyczuć różnicę między wynikającym z pierwszego wzoru czasem 0,5 s, a 0,625 s z drugiego…

No i teraz mamy zaproponowane dwa wzory, albo inaczej mówiąc dwie hipotezy opisujące czas spadku przedmiotów. Co, jeśli ponad połowa osób na sali powie, że nie wierzy w ten pierwszy wzór, a ten drugi bardziej im się podoba? Ma on bowiem niewątpliwie powab prostoty, bez żadnego pierwiastkowania czy wielu zmiennych.

Ale właściwie, czy jest to kwestia wiary, czy wiedzy..? A jeśli jednak wiedzy, to jak zweryfikować obie przedstawione hipotezy?

Tu wywiązuje się zwykle całkiem ciekawa dyskusja, którą skondensuję do wniosków należących do 3 kategorii

1. Wyprowadzenie teoretyczne

1. Pierwszy wzór można wyprowadzić z elementarnych praw fizyki, drugiego nie.
2. Czas spadku powinien zależeć od przyspieszenia – obrazowo mówiąc spadek monety na Księżycu trwałby dłużej. W tym drugim wzorze tego brakuje.
3. We wzorze muszą zgadzać się jednostki – czas ma wyjść w sekundach, jak w pierwszym wzorze; a nie w metrach, jak w drugim.

2. Doświadczenie z wcześniejszych obserwacji

4. O ile przy spadku z wysokości 1,25 m oba wzory dają zbliżony rezultat, to w przypadku wyrzucenia monety przez okno z 15. piętra (ok. 45 m nad ziemią) różnice robią się już mocno znaczące i do wychwycenia gołym okiem.
   Pierwszy wzór daje czas do upadku
   $t=\sqrt{{2 \cdot 45} \over 10}=\sqrt{90 \over 10} = \sqrt{9}=3s$
   Według obliczenia moneta spada na ziemię z prędkością 30 m/s, czyli ponad 100 km/h. Przy takim zachowaniu spadających obiektów nic dziwnego, że grono chętnych do wyskakiwania przez okno na chodnik na dole nie jest zbyt liczne…
   
   Według drugiego wzoru czas spadku monety z wysokości 45 m wyniósłby 22,5 sekundy. W zasadzie przy takim zachowaniu spadających ciał sposób wychodzenia przez okno z mieszkania na 15 piętrze, w którym znaleźlibyśmy się na dole po 22,5 sekundy (cały czas przemieszczając się ze stałą prędkością 2 m/s, czyli ok. 7 km/h) mógłby być całkiem wygodny….

3. Eksperymentalnie tu i teraz

Można przeprowadzić serię eksperymentów ze spadającymi monetami, w których z użyciem precyzyjnych urządzeń pomiarowych zmierzymy czas spadku monety z różnych wysokości i porównamy rezultaty z analizowanymi hipotezami.

Obie hipotezy możemy więc zweryfikować na wiele sposobów. Tą drugą szybko sfalsyfikujemy. Ta pierwsza będzie zaś się uparcie bronić (z dokładnością do tego, że praktyczne stosowanie wzoru jest ograniczone do pewnych warunków, takich jak np. wypełnienie sali powietrzem a nie wodą 🙂

Akt 2. U sąsiada jest cieplej niż u mnie, ale dlaczego?

Wychodząc ze swojego mieszkania w drodze do sąsiada mieszkającego w drugiej części naszego bliźniaka spoglądam na termometr na ścianie, pokazujący temperaturę 20°C. Gdy wchodzę do mieszkania sąsiada, czuję że jest u niego cieplej, co potwierdza termometr pokazujący temperaturę w mieszkaniu 24°C, jak poniżej:

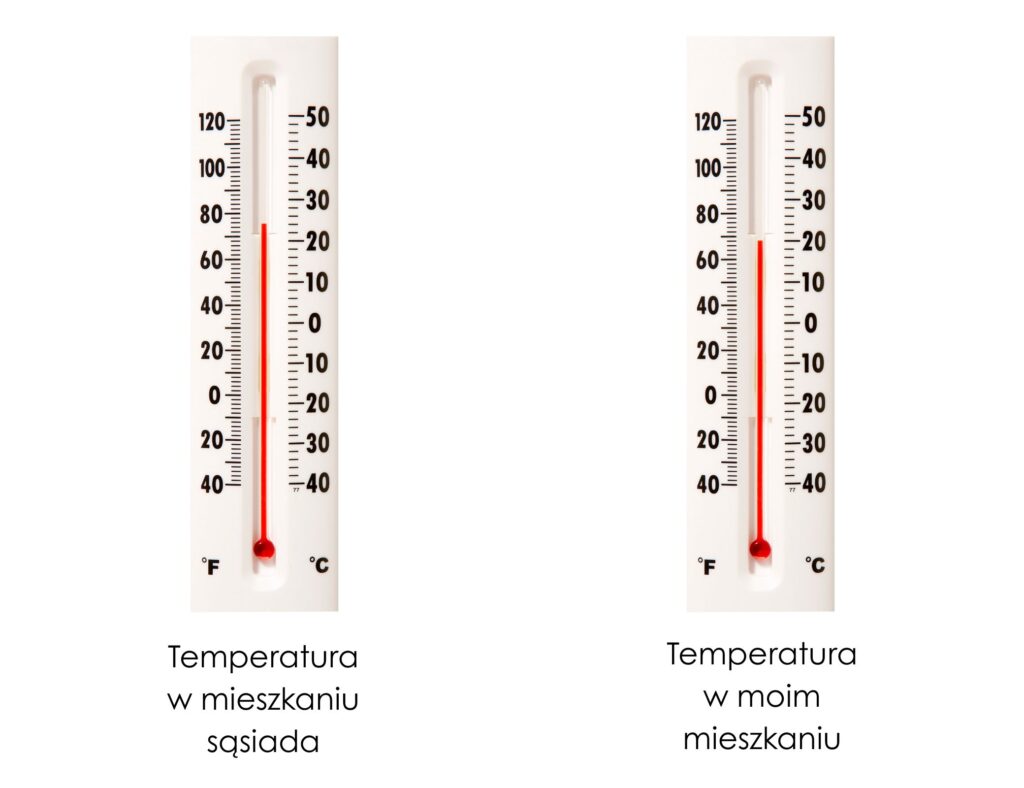
Jaka może być tego przyczyna? Dlaczego w mieszkaniu sąsiada jest cieplej niż w moim?

Zapytani uczestnicy wykładu proponują różne hipotezy:

1. może sąsiad ma mocniej rozkręcone grzejniki;
2. może w jego mieszkaniu są inne źródła ciepła, np. przez długi czas działał piekarnik;
3. może jego mieszkanie jest lepiej nasłonecznione;
4. może w jego mieszkaniu mieszka więcej osób (wydzielają ciepło);
5. może pod jego połową bliźniaka przechodzi słabo zaizolowana magistrala ciepłownicza;
6. może jego połowa bliźniaka ma lepszą izolację.

I jak je teraz sprawdzić? Czy można udzielić odpowiedzi na to pytanie, patrząc jedynie na termometry na ścianie? Nie, to nie wystarczy.

A więc? A więc należy wykonać też inne pomiary. Możemy na przykład sprawdzić temperaturę grzejników (tudzież zużycie energii na liczniku systemu ciepłowniczego), zmierzyć rozkład temperatury w pomieszczeniach (w pokoju, kuchni i ew. miejscach innych źródeł ciepła), sprawdzić nasłonecznienie, liczbę mieszkańców, temperaturę gruntu w różnych miejscach w sąsiedztwie budynku, obejrzeć obraz budynku w kamerze termowizyjnej itd. W miarę potrzeb pomiary te można prowadzić przez dłuższy czas, żeby wyeliminować możliwość, że ten jeden jedyny pomiar u sąsiada zrobiliśmy, gdy przez 3 godziny piekł coś w piekarniku i gotował na wszystkich palnikach. No i wreszcie można też zapytać sąsiada ile osób u niego mieszka lub czy zrobił termomodernizację domu.

Powiedzmy, że robimy to wszystko i stwierdzamy, że:

1. sąsiad z drugiej połowy bliźniaka ma takie same grzejniki jak my i… są one chłodniejsze niż u nas, a zużycie ciepła pokazywane przez licznik jest niższe;
2. temperatura w kuchni jest taka sama jak w salonie i innych pokojach, a sąsiad mówi, że nic ostatnio nie gotował, innych źródeł ciepła zaś nie ma;
3. jego mieszkanie ma okna ustawione tak samo jak nasze mieszkanie, na zewnątrz nie ma nic zacieniającego, czy to drzew czy budynków, w obu mieszkaniach okna są bez rolet czy zasłon, a kolor wykładziny ma podobny jak my (ma to znaczenie dla pochłaniania ciepła słonecznego);
4. sąsiad mieszka sam;
5. pomiary temperatury gruntu wokół budynku na głębokości do 1 m pokazują, że jest ona taka sama zarówno przy połówce bliźniaka należącej do sąsiada jak przy naszej;
6. zdjęcia budynku: zwykłe i w kamerze termowizyjnej wyglądają jak poniżej
   Obraz z kamery termowizyjnej wyraźnie pokazuje chłodniejsze ściany połówki sąsiada (pomimo wyższej temperatury powietrza w jego mieszkaniu). Ponieważ przy stałej temperaturze w środku ilość dostarczanego do budynku ciepła musi być równe ilości ciepła uciekającego, rejestrowana przez kamerę termowizyjną niższa temperatura ścian po stronie sąsiada oznacza, że do jego części bliźniaka dostarczamy mniej energii cieplnej.

Możemy teraz zabawić się w detektywów, weryfikując zgodność hipotez z obserwacjami. W kolumnach umieściliśmy nasze hipotezy, a w wierszach obserwacje.

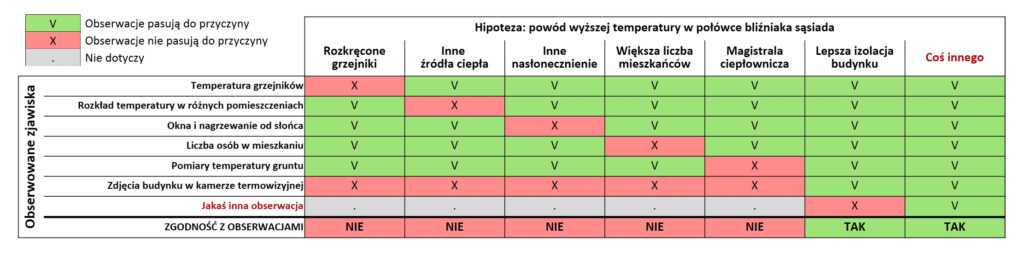
W komórkach dla każdej obserwacji odnotowaliśmy jej zgodność z daną hipotezą: zielone pola oznaczają, że hipoteza może być zgodna z obserwacją, czerwone zaś, że obserwacja sfalsyfikowała nam daną hipotezę. Aby przyjąć, że hipotezę nie została sfalsyfikowana (czyli jest niezgodna z obserwacjami), wystarczy jedna niezgodna z nią obserwacja.

W naszym przypadku jedyną hipotezą, która przetrwała weryfikację (podsumowanie w dolnym wierszu) jest lepsza izolacja budynku po stronie sąsiada. Prawdziwym “kilerem” alternatywnych hipotez są zdjęcia termowizyjne, pokazujące że z połowy budynku należącej do sąsiada ucieka mniej energii – a że przy stałej temperaturze w środku strumień energii uciekającej z budynku jest równy strumieniowi energii do niego dostarczanej, sfalsyfikowane zostały wszystkie hipotezy zakładające dostarczanie do wnętrza budynku większej ilości ciepła.

A, i jeszcze… zapytany o termomodernizację sąsiad potwierdził jej wykonanie, zachwalając przy tym wynikający z niej olbrzymi spadek rachunków za ciepło.

Nasza hipoteza mówiąca, że u sąsiada jest cieplej, bo ma lepszą izolację została potwierdzona na wiele sposobów i nie mamy na widoku żadnej hipotezy alternatywnej. W języku nauki mówimy, że tak wszechstronnie zweryfikowana hipoteza to teoria naukowa (choć w przypadku sąsiada, który ocieplił sobie dom, to może ciut zbyt górnolotne określenie… 🙂

Wyobraź sobie, że teraz przychodzi ten sam gościu, który zaproponował wzór na spadek monety t=12h, i twierdzi, że to wcale nie tak, lecz sąsiad kradnie ciepło i celowo sfałszował pomiary licznika, a na swoją obronę opowiada że to niby termomodernizacja zmniejszyła mu rachunki… Gdyby jedynymi informacjami, którymi dysponujesz było to, że u sąsiada jest cieplej, a rachunki ma niższe, te zarzuty mogłyby wyglądać poważnie. Jednak przeczy temu szereg innych obserwacji, którymi dysponujemy, możemy więc spokojnie potraktować to jako nie trzymającą się kupy teorię spiskową.

Czy to znaczy, że w ogóle nie może już być żadnej dyskusji na ten temat i nie można postawić już żadnej innej hipotezy? Ależ można, pamiętając jednak o tym, że aby zasiąść na tronie wyjaśniającej zjawisko teorii naukowej powinna być ona w pełni zgodna z różnymi obserwacjami, a do tego wcześniej zajmująca to miejsce hipoteza powinna zostać sfalsyfikowana przez pomiary. W naszej tabelce zobaczylibyśmy to jako kolejny wiersz obserwacji, niezgodnej z hipotezą lepszej izolacji budynku, ale zgodną z nową hipotezą (która powinna być też zgodna ze wszystkimi innymi obserwacjami, dając kolumnę zieloną od góry do dołu).

Akt 3. Ocieplająca się Ziemia

W Akcie 2 samo patrzenie na termometr nie pozwala powiedzieć, jaka jest przyczyna tego, że u sąsiada jest cieplej – trzeba było wykonać inne pomiary.

Podobnie, samo odnotowanie wzrostu temperatury powierzchni Ziemi (od epoki przedprzemysłowej w drugiej połowie XIX wieku o ok. 1,5°C) nie pozwala powiedzieć, jaka jest tego przyczyna. Może Słońce świeci mocniej? Może zmieniła się orbita Ziemi? Może zmieniła się aktywność wulkaniczna? Może zmieniło się natężenie promieniowania kosmicznego wpływające na zachmurzenie? A może wzrósł strumień energii płynącej z wnętrza Ziemi? Albo może wzrost stężenia gazów cieplarnianych spowodował spadek strumienia energii uciekającego w przestrzeń kosmiczną? 

Można postawić wiele alternatywnych hipotez. Jak je zweryfikować?

Rzecz jasna trzeba wykonać inne pomiary, wchodząc w rolę detektywa i tworząc zestawienie zgodności naszych hipotez z szeregiem różnorodnych obserwacji.

Przykładowo: jeśli wzrost temperatury byłby związany ze wzrostem dopływu energii ze Słońca powinniśmy obserwować m.in.:

• wzrost średniej temperatury atmosfery przy powierzchni Ziemi;
• wzrost średniej temperatury wyższych warstw atmosfery i jej „puchnięcie”;
• szybsze nagrzewanie się szerokości geograficznych otrzymujących najwięcej energii ze Słońca (tropiki);
• szybsze nagrzewanie się wód powierzchniowych oceanów w tropikach;
• nagrzewanie się wód oceanów od powierzchni w głąb;
• wzrost strumienia energii dopływającej ze Słońca (pomiary satelitarne i naziemne);
• wzrost strumienia energii uciekającej w przestrzeń kosmiczną (pomiary satelitarne).

Gdyby zaś wzrost temperatury był związany ze wzrostem stężenia gazów cieplarnianych powinniśmy obserwować m.in. (odnieśmy się do tych samych punktów):

• wzrost średniej temperatury atmosfery przy powierzchni Ziemi;
• spadek średniej temperatury wyższych warstw atmosfery i jej „kurczenie się”;
• wyrównywanie temperatury między różnymi szerokościami geograficznymi (szybsze ocieplanie się rejonów polarnych);
• szybsze nagrzewanie się wód powierzchniowych oceanów w rejonach polarnych;
• nagrzewanie się wód oceanów od powierzchni w głąb;
• brak istotnych zmian strumienia energii dopływającej ze Słońca (pomiary satelitarne i naziemne);
• spadek strumienia energii uciekającej w przestrzeń kosmiczną (pomiary satelitarne) – analogicznie spadku ilości energii uciekającej z ocieplonego budynku.

Po porównaniu z obserwacjami nasza tabelka wyglądałaby tak:

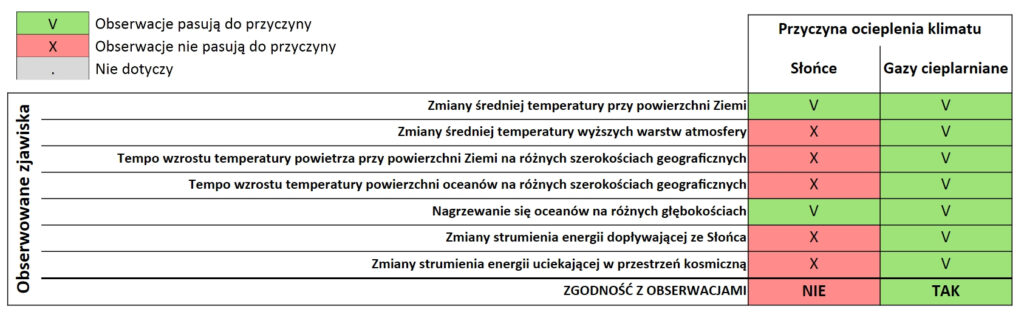
W podobny sposób można sprawdzić zgodność innych hipotez z obserwacjami, i naukowcy rzecz jasna to zrobili – wielokrotnie, dla wielu potencjalnych hipotez i mnóstwa obserwacji. I nie wymyślono żadnej alternatywnej hipotezy, która pasowałaby do obserwacji zachodzącej zmiany klimatu. Nie znaleziono też żadnych obserwacji, które falsyfikowałyby teorię globalnego ocieplenia spowodowanego emisjami gazów cieplarnianych przez ludzkość.

A, i jeszcze jedno… w Akcie 1 odnotowaliśmy trzy sposoby na weryfikację hipotezy:

1. Wyprowadzenie teoretyczne.
2. Doświadczenie z wcześniejszych obserwacji.
3. Eksperymentalnie tu i teraz.

Mają one także zastosowanie w przypadku obserwacji zmiany klimatu.

1. Wyprowadzenie teoretyczne
   Temperatura powierzchni Ziemi jest kwestią fizyki. Rola gazów cieplarnianych w jej podwyższaniu jest znana od XIX wieku. Już wtedy też naukowcy przewidywali ocieplenie klimatu związane ze spalaniem paliw kopalnych. Więcej na ten temat przeczytasz w artykule Historia Badań Klimatu. Od tego czasu nasze zrozumienie zmiany klimatu, bazujące na wiedzy o prawach fizyki i różnorodnych obserwacjach stało się równie dobre (o ile nie lepsze) niż w przypadkach monety i mieszkania sąsiada opisanych w poprzednich Aktach. 
   I – analogicznie jak w historii wzoru na czas spadania monety – nawet jeśli ktoś nie wie, jak przeprowadzić odpowiednie obliczenia, to są tacy, którzy to potrafią.
2. Doświadczenie z wcześniejszych obserwacji
   Klimat Ziemi zmieniał się w przeszłości: od chłodnych epok lodowych skuwających terytorium Polski grubym na ponad kilometr lądolodem po okresy tak ciepłe, że w Oceanie Arktycznym pływały krokodyle. I wiemy dlaczego tak było i jaką rolę grały w tym inne czynniki, od Słońca po gazy cieplarniane w atmosferze. Patrz: Klimat dawnych epok: od dinozaurów do lądolodu.
3. Eksperymentalnie tu i teraz
   Obecną zmianę klimatu obserwujemy na bieżąco – mamy bezpośrednie różnorodne pomiary z powierzchni ziemi, oceanów i satelitów. I wszystkie te obserwacje są zgodne z sygnaturą ocieplenia klimatu wywoływanego wzrostem stężenia gazów cieplarnianych w atmosferze. Tabelkę z zestawieniem zgodności różnych alternatywnych hipotez przyczyn ocieplania się klimatu z obserwacjami znajdziesz w artykule Ziemia się nagrzewa i wiemy dlaczego.

Rzecz jasna wciąż doszlifowujemy detale wiedzy na temat dawnych zmian klimatu, prognoz dotyczących zachowania chmur czy cyrkulacji oceanicznej w ocieplającym się klimacie, podobnie jak mogliśmy szlifować wzór podany w Akcie 1. Ale z praktycznego punktu widzenia nie zmienia to znacząco całego obrazu.

Czy to wszystko znaczy, że znalezienie alternatywnej hipotezy czy obserwacji falsyfikujących obecny konsensus naukowy jest niemożliwe? Oczywiście nie, podobnie jak w przypadku opisanej w Akcie 2 przyczyny tego, że u sąsiada jest cieplej. Tyle, że jest to ekstremalnie mało prawdopodobne.

Jest naszą naturalną ludzką cechą, że gdy zderzamy się z czymś takim jak powodowana przez nas zmiana klimatu, która jest tematem mocno naukowym, w swoich konsekwencjach przerażającym i czymś nad czym pojedyncza osoba nie ma kontroli, naszą odruchową reakcją psychologiczną jest wyparcie. Nie dlatego ludzie nie „wierzą” w antropogeniczne globalne ocieplenie, bo znają się na transferze energii w atmosferze i fizyce chmur lepiej od zajmujących się tym fizyków, czy na dawnym klimacie lepiej od paleoklimatologów. Robią to dlatego, że jest to wiedza bardzo niewygodna. Problem w tym, że – napiszę to jako fizyk w tekście poświęconym w lwiej części fizyce – prawa fizyki mają w bardzo głębokim poważaniu to, że coś jest dla nas niewygodne, tylko robią swoje.

A więc? 

A więc podejmując ważne decyzje zdecydowanie mądrzej jest kierować się wiedzą, a najlepiej najlepszą dostępną wiedzą naukową.