Jak wzrost koncentracji gazów cieplarnianych wpływa na widmo promieniowania ziemskiego a przez to na bilans energetyczny (radiacyjny) Ziemi? Jakie znaczenie ma wyjściowa koncentracja gazu cieplarnianego? Czemu metan jest groźniejszy niż dwutlenek węgla? Co to jest ekwiwalent dwutlenku węgla?
Cykl „Efekt cieplarniany dla średniozaawansowanych”:
Termiczna struktura atmosfery
Gazy cieplarniane i ich cechy
Wpływ gazów cieplarnianych na widmo promieniowania ziemskiego
Zmiany koncentracji gazów cieplarnianych a transport energii
Wpływ chmur
Aerozole
Bilans energetyczny Ziemi
Średnia zawartość cząsteczek pary wodnej w atmosferze wynosi obecnie ok. 4000 ppm, dwutlenku węgla ok. 400 ppm, a metanu 2 ppm. Jednak względne różnice ich wpływu na efekt cieplarniany (patrz tabela 1. w trzeciej części cyklu) są znacznie mniejsze od względnych proporcji ich zawartości w atmosferze. Jest to związane przede wszystkim z tym, że mała liczba cząsteczek w atmosferze jest proporcjonalnie bardziej skuteczna w pochłanianiu promieniowania niż taka sama liczba dodana do atmosfery, w której już jest sporo danego gazu cieplarnianego. Ten ostatni efekt jest związany z nasycaniem się pasm absorpcyjnych. Przyjrzyjmy się temu bliżej.
Nasycanie się pasm absorpcyjnych
Spójrzmy, jak zmienia się widmo promieniowania, gdy zwiększamy stężenie gazów cieplarnianych. Do zobaczenia „co by było gdyby”, wykorzystamy znany nam już model Uniwersytetu w Chicago. Sprawdzimy, jak zmieni się opuszczające Ziemię promieniowanie przy różnych stężeniach CO2: bez tego gazu, przy stężeniu 10 ppm (cząsteczek na milion cząsteczek powietrza), 200 ppm, 400 ppm, 800 ppm i 1600 ppm.
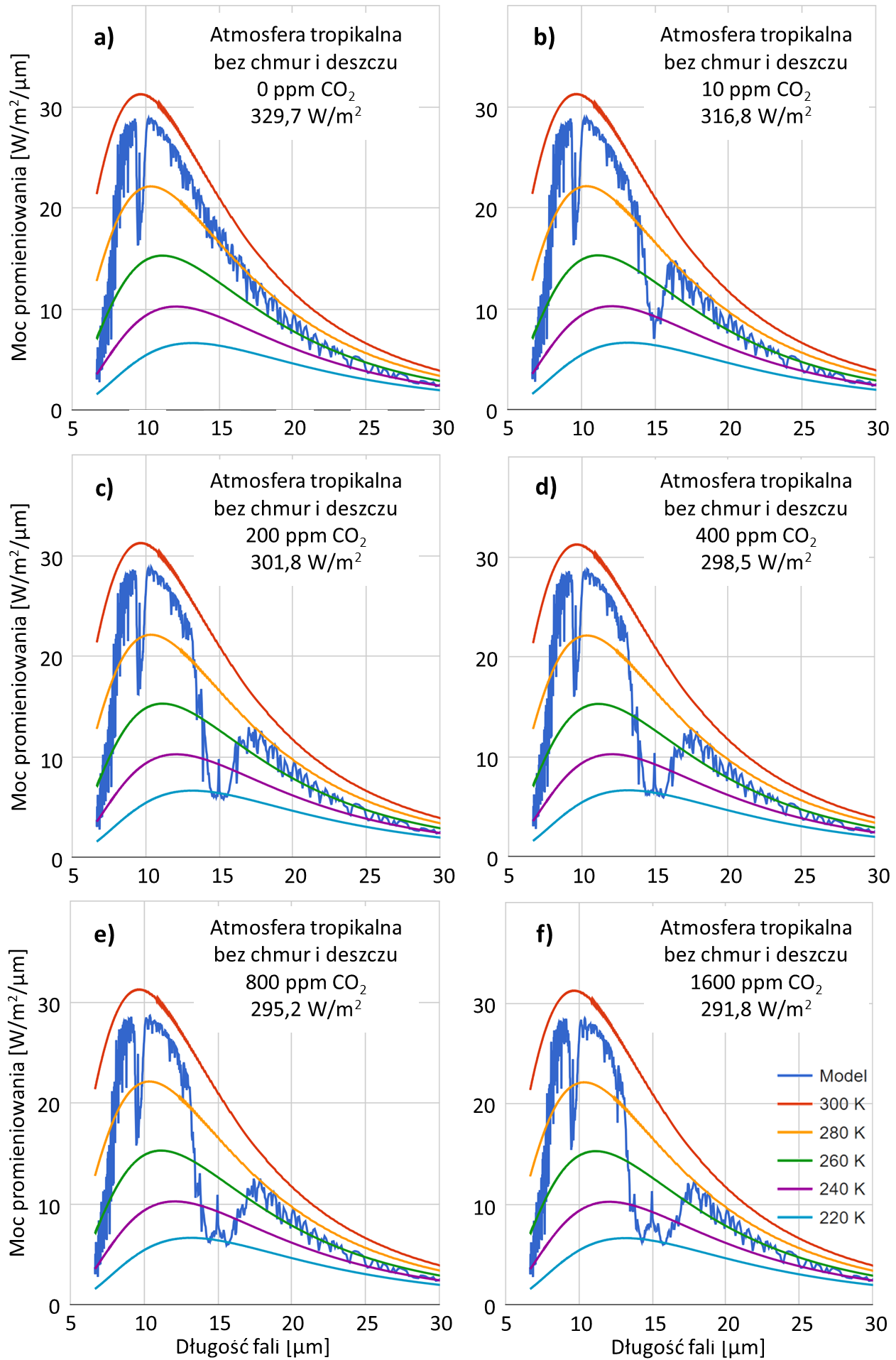
Gdyby w atmosferze nie było w ogóle cząsteczek CO2 (rysunek 2a), byłaby ona praktycznie przezroczysta dla promieniowania o długości fali ok. 15 μm, podobnie jak jest w oknie atmosferycznym (czyli zakresie 10–12 μm). Pokazuje to wykres widma promieniowania ziemskiego dla długości fal powyżej 10 μm opadający łagodnie, bez większych odstępstw od dzwonowatego kształtu.
Dodanie już zaledwie 10 ppm CO2 (rysunek 2b) powoduje wyraźną zmianę widma opuszczającego Ziemię promieniowania. Przy tej samej temperaturze powierzchni jego strumień spada z 329,7 do 316,8 W/m2, czyli o 12,9 W/m2. W okolicach 15 μm pojawia się wyraźny „dołek” w widmie, co świadczy o tym, że fale tej długości zaczęły być pochłaniane.
Dalsze zwiększenie koncentracji CO2 do 200 ppm (rysunek 2c), co odpowiada stężeniu z czasów maksimum epok lodowych, powoduje spadek strumienia opuszczającej Ziemię energii do 301,8 W/m2. „Dołek” w widmie pogłębił się i widzimy, że promieniowanie w zakresie 14–16 μm pochodzi z wysokości odpowiadającej najniższej w atmosferze temperaturze 220 K (widmo promieniowania ziemskiego styka się tu z zaznaczonym kolorem jasnoniebieskim widmem ciała doskonale czarnego o tej temperaturze). Uwagę zwraca też to, że dla długości 15 μm, dla której pochłanianie przez CO2 jest najintensywniejsze, obserwowana temperatura jest wyższa („szpileczka” pośrodku dołka). To sygnał, że pochodzi ono z obszaru o wyższej temperaturze (powyżej tropopauzy temperatura rośnie wraz z wysokością).
Wykresy 2d–f to seria trzech podwojeń stężeń CO2: 200 ppm → 400 ppm → 800 ppm → 1600 ppm. Widać, że minimum widma związane z pochłanianiem podczerwieni przestaje się pogłębiać. To właśnie nazywamy nasyceniem pasma absorpcyjnego – więcej fal tej długości po prostu nie może już zostać pochłonietych. Czy to oznacza, że w pewnym momencie dodawanie kolejnych porcji gazów cieplarnianych przestanie mieć znaczenie? Nie. Zauważmy, że chociaż „dołek” w widmie przestał się pogłębiać, to jednak cały czas się poszerza, a opuszczający Ziemię strumień energii systematycznie spada – z każdym podwojeniem o około 3,4 W/m2 (zależność ta jest dobrze spełniona dla zakresu 10–30000 ppm).
Po nasyceniu pasma absorpcyjnego wciąż może się ono jeszcze poszerzać.
Koncentracje gazów cieplarnianych a bilans radiacyjny Ziemi
Zmiany strumienia opuszczającej Ziemię energii w zależności od atmosferycznej koncentracji CO2 możemy przedstawić na wykresie.
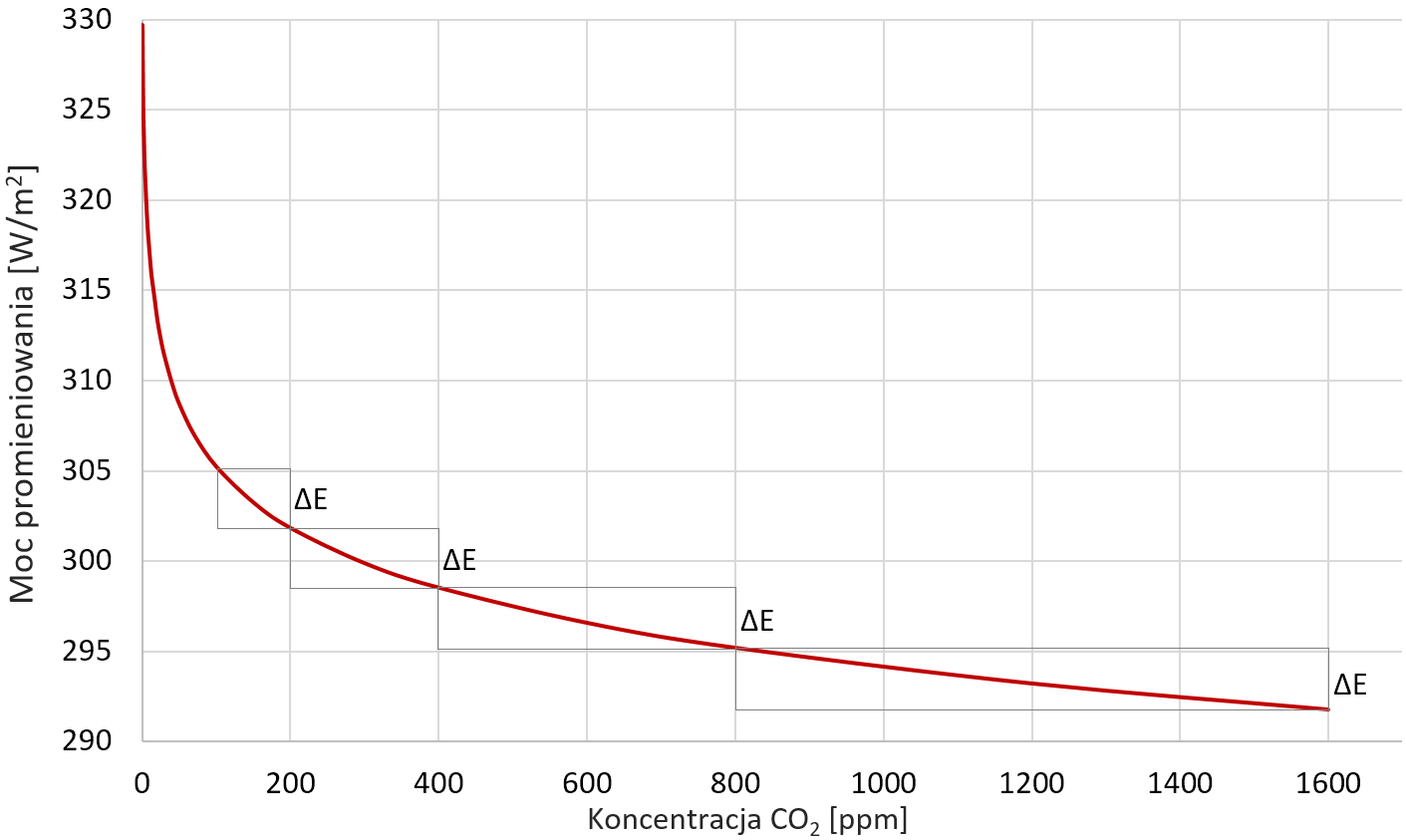
Bardzo istotne jest spostrzeżenie, że dla interesującego nas przedziału (od 200 ppm do tysięcy ppm) każde podwojenie stężenia dwutlenku węgla przekłada się na taką samą zmianę strumienia opuszczającej Ziemię energii, niezależnie od tego, czy jest to wzrost z 200 ppm do 400 ppm, czy z 800 do 1600 ppm.
Zależność, w której podwojenie wartości x skutkuje stałą zmianą wartości y, to zależność logarytmiczna.
Naszą symulację przeprowadziliśmy dla określonych warunków (średnioroczna atmosfera dla regionu zwrotników). Średnio rzecz biorąc, podwojenie stężenia CO2 dla całej planety skutkuje zmniejszeniem opuszczającego Ziemię promieniowania o 3,7 W/m2 (w przybliżonych rachunkach często stosowana jest też wartość 4 W/m2).
Zmianę strumienia energii ΔE w W/m2 w funkcji koncentracji CO2 (czyli wymuszenie radiacyjne dwutlenku węgla względem określonego poziomu odniesienia) możemy opisać wzorem:
ΔECO2 = 3,7·ln(pCO2/p0CO2)/ln(2) = 5,35·ln(pCO2/p0CO2) (1)
Bardziej precyzyjna zależność, w szczególności w zakresie wyższych koncentracji, ma postać:
ΔECO2 = 5,35·ln(pCO2/p0CO2) + 0,39·(ln(pCO2/p0CO2))2 (2)
gdzie pCO2 to koncentracja CO2 w atmosferze, a p0CO2 – poziom odniesienia, względem którego mierzymy różnicę strumienia energii, zazwyczaj w obliczeniach jest to 280 ppm, odpowiadające stężeniu CO2 w epoce przedprzemysłowej.
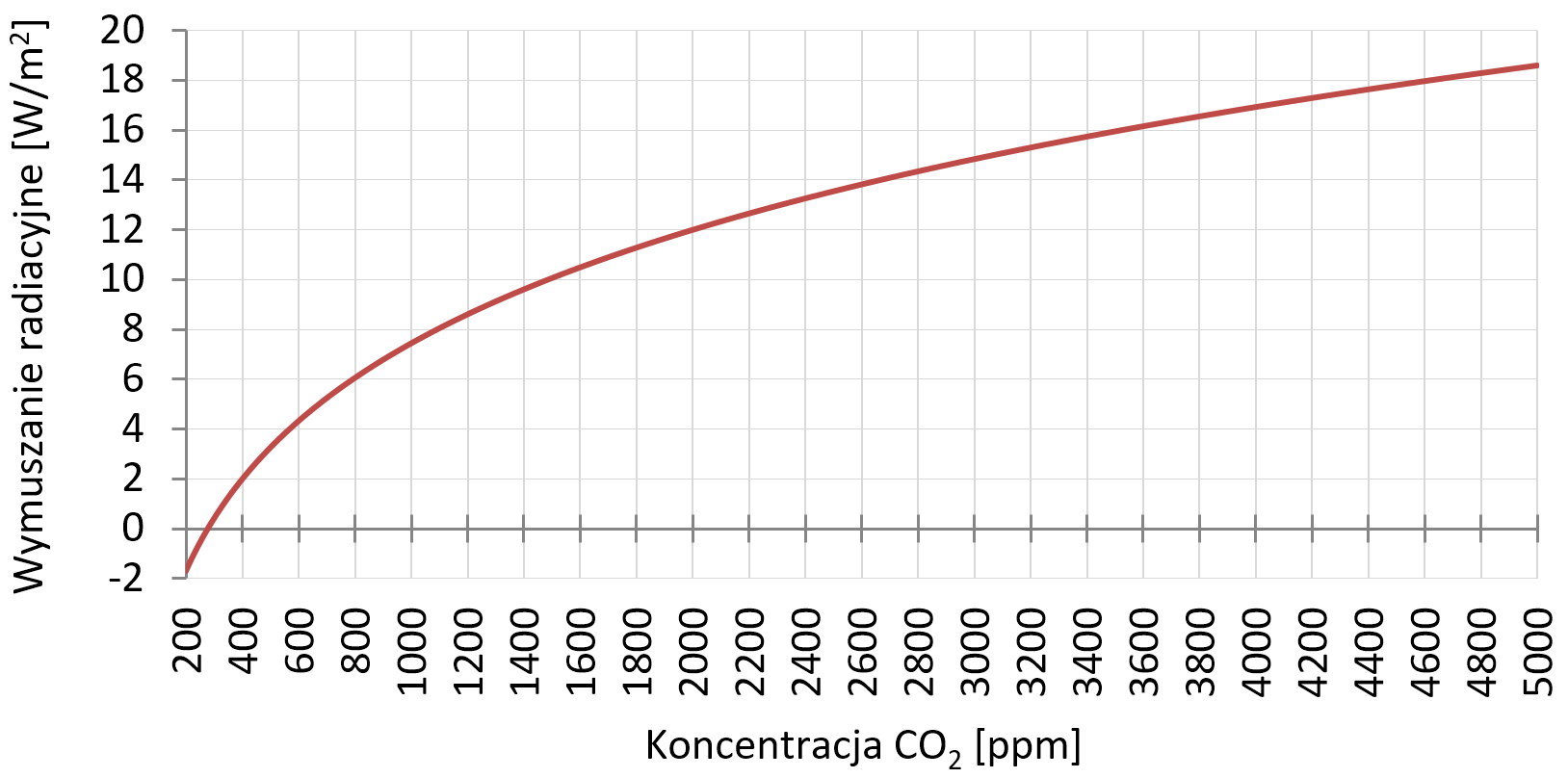
Zobaczmy, który gaz cieplarniany działa silniej: dwutlenek węgla czy metan. Na rysunku 5 widzimy porównanie zależności strumienia opuszczającej Ziemię energii od stężenia każdego z tych gazów (przy zerowym stężeniu drugiego).
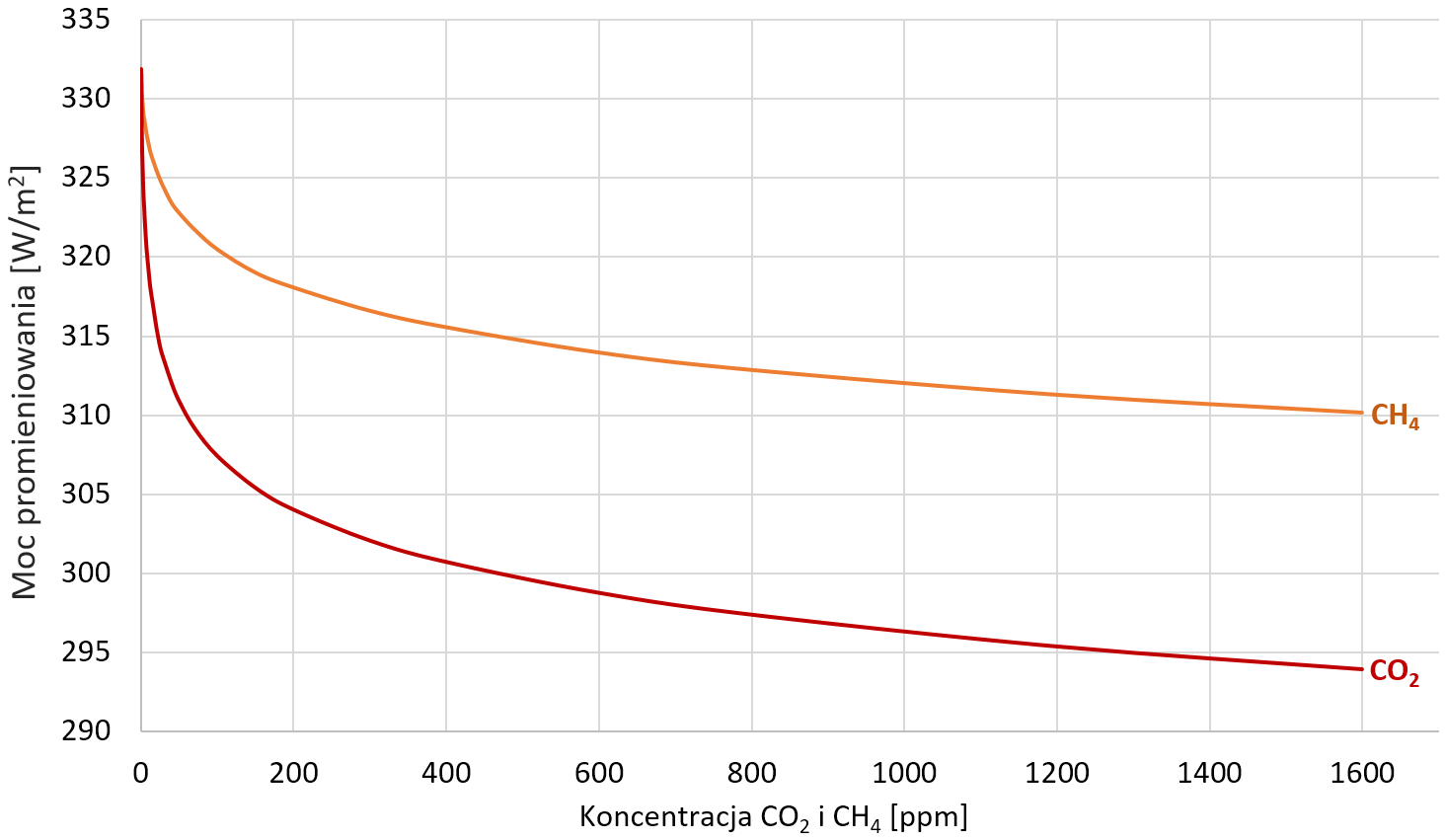
Widać, że przy tej samej koncentracji dwutlenku węgla i metanu większy wpływ na bilans radiacyjny planety (a więc też temperaturę i widmo promieniowania powierzchni Ziemi) ma dwutlenek węgla. Aby uzyskać ten sam efekt radiacyjny, co dla koncentracji metanu wynoszącej 1000 ppm, koncentrację dwutlenku węgla wystarczy zwiększyć do niecałych 40 ppm.
Dlaczego więc uważa się, że metan jest silniejszym gazem cieplarnianym od dwutlenku węgla?
To skrót myślowy związany z tym, że obecne stężenie CH4 jest ponad 200 razy mniejsze niż CO2 (w 2018 roku ok. 1,9 ppm vs. 406 ppm), więc pasma absorpcyjne CH4 nie są jeszcze nasycone. Zwiększenie stężenia CH4 o 1 ppm, z 1 ppm do 2 ppm zmienia bilans radiacyjny planety o ok. 0,6 W/m2, podczas gdy wzrost stężenia CO2 o 1 ppm (dla obecnej koncentracji 400 ppm: z 400 do 401 ppm) zmienia bilans zaledwie o ok. 0,013 W/m2: blisko 50-krotnie mniej.

Masa metanu potrzebna dla zwiększenia koncentracji o 1 ppm jest blisko trzykrotnie mniejsza od masy dwutlenku węgla (ponieważ masa 1 mola CO2 wynosi 44 gramów, a CH4 tylko 16 gramów – blisko trzykrotnie mniej), przeliczając więc z jednostek ppm (lub moli) na tony emisji uzyskujemy mniej więcej 130-krotnie większy wpływ metanu.
Jeśli czynnik ten wynosi 130, to dlaczego mówi się, że „metan jest gazem cieplarnianym kilkadziesiąt razy silniejszym niż dwutlenek węgla” (oczywiście, przeliczając na tony emisji)? Wynika to z tego, że metan ma krótki czas życia w środowisku – średnio zaledwie ok. 10 lat.
W ciągu ok. 7 lat połowa cząsteczek CH4 ulega reakcjom chemicznym (to tzw. czas połowicznego rozpadu t1/2) i tym samym jest usuwana ze środowiska. Po kolejnych 14 latach pozostaje ich ¼, po 21 latach 1/8 i tak dalej. Związek między czasem połowicznego rozpadu a średnim czasem życia możemy zapisać jako:
τ = t1/2 / ln(2) = 1,44 t1/2
Średni czas życia cząsteczki metanu wynosi więc około 10 lat.
Wyemitowany metan ma silne działanie w krótkim horyzoncie czasowym, lecz znacznie słabsze w długim.
Wpływ emisji gazów cieplarnianych wyrażamy w tzw. potencjale tworzenia efektu cieplarnianego (patrz ramka poniżej). Dla metanu GWP wynosi 84 w ciągu 20 lat od emisji, a im więcej czasu mija, tym bardziej spada – przez 100 lat do 28. Gdyby dodatkowo uwzględnić sprzężenia zwrotne cyklu węglowego, potencjał metanu wyniósłby odpowiednio 86 (dla 20 lat) i 34 (dla 100 lat) (IPCC, 2013).
Potencjał tworzenia efektu cieplarnianego (ang. Global Warming Potential, GWP) mówi nam, ile energii pochłonie w wybranym okresie (np. 20 lub 100 lat) wyemitowana na jego początku 1 tona gazu cieplarnianego. Punktem odniesienia jest energia pochłaniana w takim czasie przez 1 tonę dwutlenku węgla. Innymi słowy – potencjał tworzenia efektu cieplarnianego dla dwutlenku węgla z definicji zawsze wynosi 1.
Im większy GWP emitowanych gazów cieplarnianych, tym większy wpływ emisji tony gazu na ocieplenie klimatu.
Pasma absorpcyjno-emisyjne metanu i podtlenku azotu (trzeciego z „wielkiej trójki” gazów cieplarnianych emitowanych przez człowieka) nakładają się na siebie. Zależność wymuszenia radiacyjnego od koncentracji jest tu więc bardziej złożona i wymaga użycia w równaniach wartości stężeń obu gazów (odpowiednio pCH4 i pN2O). Dla metanu i podtlenku azotu mamy odpowiednio:
ΔECH4 = 0,036·(pCH41/2 – p0CH41/2) – (β(pCH4, p0N2O) – β(p0CH4, p0N2O)) (3)
ΔEN2O = 0,120·(pN2O1/2 – p0N2O1/2) – (β(p0CH4, pN2O) – β(p0CH4, p0N2O)) (4)
gdzie stężenie jest wyrażone w [ppb] (cząsteczkach na miliard cząsteczek powietrza), p0 oznacza koncentracje wyjściowe odpowiednich gazów (dla epoki przedprzemysłowej p0CH4=722 ppb, p0N2O=270 ppb), a β funkcję postaci:
β(M,N) = 0,47·ln(1 + 0,0000201 (M·N)0,75 + 5,31·10-15·M·(M·N)1,52
gdzie M i N to stężenia CH4 i N2O wyrażone w ppb.

Z kolei dla związków, których zawartość w atmosferze jest bardzo niewielka, a pasma absorpcyjne nie są nasycone, wymuszenie radiacyjne rośnie liniowo ze wzrostem ich koncentracji. Do takich gazów należą CFC, HCFC, HFC i inne gazy przemysłowe. Przykładowo dla CFC, przy wyrażeniu stężeń w [ppb]:
ΔECFCF11 = 0,25·(pCFC11 – p0CFC11) (5)
ΔECFCF12 = 0,25·(pCFC12 – p0CFC12) (6)
Ponieważ w epoce przedprzemysłowej gazów tych w ogóle nie było w atmosferze, p0CFC = 0.
Co by się stało, gdybyśmy nagle (oczywiście z punktu widzenia bezwładności cieplnej ziemskiego systemu klimatycznego) zwiększyli stężenie gazów cieplarnianych w atmosferze?
Byłby to odpowiednik pogrubienia izolacji w domu – tak jak opisaliśmy to w tekście Globalne ocieplenie: wersja dla niewtajemniczonych. W rezultacie spadłby strumień energii unoszonej przez opuszczające Ziemię promieniowanie podczerwone. Widzimy to na rysunku 8: punktem wyjścia (a) jest planeta, której atmosfera jest pozbawiona CO2. Planeta pozostaje w długoterminowej równowadze klimatycznej: absorbowana energia (pochodząca ze Słońca) jest równa wypromieniowywanej, w naszym przykładzie 329,7 W/m2. Po wzroście stężenia CO2 do 1600 ppm (pogrubienie izolacji), strumień odprowadzanej energii spada do 291,8 W/m2 (b). Ponieważ strumień docierającej ze Słońca energii jest taki jak wcześniej, system klimatyczny planety zacznie akumulować ciepło, jej temperatura będzie rosnąć, a wraz z nią wzrośnie ilość wypromieniowywanej energii, zgodnie z prawem Stefana-Boltzmanna. Kiedy ta ostatnia zrówna się ze strumieniem energii pochłanianej, sytuacja znów się ustabilizuje (c) – jednak przy wyższej temperaturze powierzchni planety (w tym przykładzie, przy ustalonej wilgotności względnej, wyższej o 13,2°C). Wyższa temperatura powierzchni planety jest wyraźnie widoczna w oknie atmosferycznym (ponad linią czerwoną odpowiadającą 300 K = 27°C): w strefie międzyzwrotnikowej robi się naprawdę gorąco.
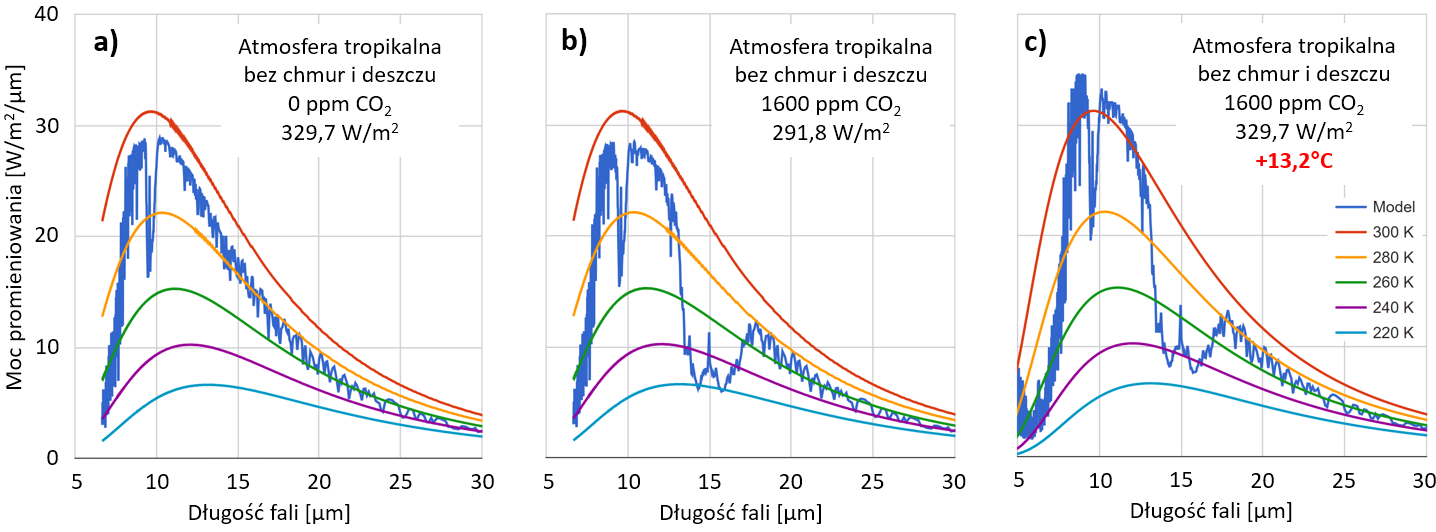
Gdy w atmosferze przybywa gazów cieplarnianych, temperatura powierzchni planety rośnie, co pozwala przywrócić równowagę radiacyjną.
Poziom emisji
Wysokość, z której średnio rzecz biorąc promieniowanie podczerwone ucieka w przestrzeń kosmiczną, nazywamy „poziomem emisji”. Wzrost temperatury, spowodowany wyższym stężeniem gazów cieplarnianych, możemy postrzegać w kontekście wysokości, z której emitowane jest uciekające w kosmos promieniowanie podczerwone oraz gradientu temperatury dyktowanego przez równowagę radiacyjno-konwekcyjną.
Temperaturę emisyjną Ziemi oszacowaliśmy na 256 K, co przy średniej temperaturze rzeczywistej powierzchni Ziemi równej 289 K daje nam różnicę 33 K. Na jakiej wysokości w atmosferze temperatura jest o 33 K niższa niż temperatura powierzchni Ziemi? Przy spadku temperatury wraz z wysokością 6°C/km jest to wysokość H = 33/6 km = 5,5 km. Obserwator patrzący na Ziemię z kosmosu nie dostrzega promieniowania emitowanego przez samą powierzchnię planety – jest ono w znacznej mierze pochłaniane przez zalegające nad nią gazy cieplarniane. Promieniowanie, które ucieka w kosmos, jest przede wszystkim emitowane przez wyższe warstwy atmosfery, w przybliżeniu właśnie od wysokości ok. 5,5 km.

Zwiększając stężenie gazów cieplarnianych w atmosferze, spowodujemy, że stanie się ona nieprzezroczysta dla podczerwieni do większej wysokości, a poziom emisji będzie się wtedy znajdował wyżej. Powiedzmy, że na wysokości 6,5 km. Jakie zmiany spowoduje to w atmosferze i na powierzchni Ziemi? Jeśli planeta ma pozostać w stanie równowagi i emitować tyle samo promieniowania, ile otrzymuje od Słońca, jej temperatura emisyjna powinna pozostać bez zmian. To znaczy, że teraz to na wysokości 6,5 km powietrze powinno mieć temperaturę równą temperaturze emisyjnej Ziemi (256 K). Aby to było możliwe, ogrzać muszą się wszystkie warstwy powietrza poniżej oraz powierzchnia Ziemi. Jeśli przyjmiemy zmiany temperatury z wysokością w tempie 6 K/km, oznacza to wzrost temperatury powierzchni planety o 6 K.
Wzrost koncentracji gazów cieplarnianych można rozumieć jako przesunięcie poziomu emisji na większą wysokość. Powoduje to wzrost temperatury leżących poniżej warstw atmosfery, a także powierzchni Ziemi.
A jak to wygląda na innych planetach?
Na Wenus gęsta atmosfera, składająca się głównie z dwutlenku węgla, wypromieniowuje podczerwień ze średniej wysokości kilkudziesięciu kilometrów (poziom emisji). Ze względu na brak pary wodnej, gradient wynikający z równowagi radiacyjno-konwekcyjnej jest bliski gradientowi suchoadiabatycznemu (10°C/km), w rezultacie czego temperatura powierzchni planety jest o kilkaset stopni wyższa od temperatury emisyjnej (patrz tabela 1 w artykule Efekt cieplarniany – jak to działa). Czy w takim razie, gdyby Słońce zgasło i temperatura emisyjna spadłaby do temperatury promieniowania tła (3 K), to na powierzchni Wenus nadal cały czas byłoby tak gorąco? Oczywiście nie. Z planety uciekałoby więcej energii, niż by do niej docierało (praktycznie zero), a w miarę utraty przez planetę energii dochodziłoby do „osiadania” i przebudowy atmosfery, aż wreszcie temperatura spadłaby na tyle, że obecny dziś w atmosferze Wenus dwutlenek węgla zestaliłby się i spadł na powierzchnię.
Z kolei na Marsie, pomimo braku pary wodnej, spadek temperatury w troposferze jest rzędu zaledwie 3–4°C/km, co wiąże się z obecnością absorbującego promieniowanie pyłu. Ponieważ na Marsie burze pyłowe nie są stanem permanentnym, stąd i gradient temperatury przyjmuje wartości pośrednie (zresztą mocno zależny od zapylenia atmosfery w danym momencie, a przez to zmienny w czasie).
Bardziej szczegółowe wyjaśnienie działania efektu cieplarnianego na Wenus i Marsie znajdziesz w artykule Efekt cieplarniany na Ziemi, Wenus i Marsie.
Nisko – grzeje, wyżej – chłodzi
Zwiększenie koncentracji dwutlenku węgla (albo innego gazu cieplarnianego o niezmieniającej się wraz z wysokością koncentracji) powoduje wzrost temperatury przy powierzchni Ziemi. Jednocześnie jednak powoduje… spadek temperatury w stratosferze i wyższych warstwach atmosfery. Dlaczego?
Przy wyższej koncentracji CO2 więcej promieniowania o długościach fal odpowiadających pasmom absorpcyjnym CO2 będzie pochłaniane przy powierzchni Ziemi. Pochłonąwszy tę energię, wzbudzone cząsteczki CO2 będą przekazywać tę energię poprzez zderzenia innym cząsteczkom, w tym azotu i tlenu, podnosząc tym samym temperaturę przypowierzchniowych warstw atmosfery. Skoro więcej promieniowania o tych długościach fal zostanie pochłonięte przy powierzchni, mniej przedostanie się wyżej, dostarczając w ten sposób mniej energii na większe wysokości – co będzie powodować ich ochładzanie się.
Dodatkowo, część energii pochłoniętej przez gazy przy powierzchni Ziemi będzie wypromieniowywana w postaci fal niepodlegających absorpcji przez gazy cieplarniane (np. mających długości z zakresu okna atmosferycznego). Ta zamiana spowoduje, że część energii, która przeniknie do wyższych warstw atmosfery, nie będzie mogła zostać przez nie pochłonięta i przysłużyć się ich ociepleniu.

Dla zwizualizowania zachodzących zmian skorzystajmy z analogii ocieplanego budynku, do którego dostarczamy stały strumień ciepła (tak jak we wspomnianym już tekście Globalne ocieplenie: wersja dla niewtajemniczonych). Jak zmieni się temperatura pod tynkiem zewnętrznym (naszym odpowiednikiem górnych warstw atmosfery), gdy między murem a tynkiem pojawi się gruba warstwa izolacji? Spadnie – prawie do temperatury panującej na zewnątrz. Nawet gdy temperatura w budynku w końcu wzrośnie, a przepływający przez ściany strumień energii wróci do pierwotnej wielkości, temperatura pod tynkiem będzie niższa niż przed założeniem izolacji. Zwiększając koncentrację gazów cieplarnianych, powinniśmy więc obserwować wzrost temperatury w niskiej troposferze oraz spadek w stratosferze i wyższych warstwach atmosfery.
Możemy na to zjawisko spojrzeć w jeszcze inny sposób. W stanie równowagi strumienie energii słonecznej pochłanianej przez planetę i wypromieniowanej w kosmos są równe. Jeśli zwiększymy zawartość CO2 w atmosferze i poczekamy na ustabilizowanie się sytuacji, jak zmienią się temperatury na różnych wysokościach? Przy powierzchni temperatura oczywiście wzrośnie, a co się będzie działo na większej wysokości? Skoro strumień opuszczającej planetę energii na początku i końcu ma być taki sam (równy strumieniowi energii pochłanianej), a na końcu dolne (cieplejsze teraz) warstwy atmosfery wypromieniowują więcej energii, to górne warstwy muszą wypromieniowywać mniej – czyli muszą być chłodniejsze.
Jest jeszcze jeden mechanizm, za pomocą którego wzrost stężenia dwutlenku węgla wpływa na chłodzenie wysokich warstw atmosfery. W troposferze cząsteczki zderzają się bardzo często, więc wzbudzona w wyniku pochłonięcia promieniowania cząsteczka nie zdąży wypromieniować pochłoniętej energii, lecz pozbędzie się jej podczas zderzenia, zamieniając na energię kinetyczną ruchu (co podniesie temperaturę gazu). W górnych warstwach atmosfery – mezosferze i znajdującej się nad nią termosferze – powietrze jest już tak rozrzedzone, że cząsteczki zderzają się bardzo rzadko. Gdy więc w wyniku zderzenia cząsteczka znajdzie się w stanie wzbudzonym, ma bardzo niewielkie szanse na szybkie oddanie energii innej cząsteczce. W takich warunkach cząsteczki CO2 pochłoniętą podczas zderzeń energię kinetyczną wypromieniowują we wszystkie strony (a połowa dostępnych kierunków wyprowadza foton w przestrzeń kosmiczną), w rezultacie chłodząc najwyższe warstwy atmosfery. Wzrost stężenia CO2 w mezosferze i termosferze (dla gazu dobrze wymieszanego zachodzi on proporcjonalnie do zmian przy powierzchni Ziemi) prowadzi więc do wzmożonego ochładzania najwyższych warstw atmosfery, która w związku z tym „osiada”. W rezultacie gęstość powietrza na ustalonej wysokości w górnych warstwach atmosfery się zmniejsza.
Czytaj dalej – o znaczeniu chmur w bilansie energetycznym Ziemi.
Artykuł jest przeredagowanym na potrzeby publikacji w internecie fragmentem książki Marcina Popkiewicza, Aleksandry Kardaś i Szymona Malinowskiego pt. Nauka o klimacie.
Fajnie, że tu jesteś. Mamy nadzieję, że nasz artykuł pomógł Ci poszerzyć lub ugruntować wiedzę.
Nie wiem, czy wiesz, ale naukaoklimacie.pl to projekt non-profit. Tworzymy go my, czyli ludzie, którzy chcą dzielić się wiedzą i pomagać w zrozumieniu zmian klimatu. Taki projekt to dla nas duża radość i satysfakcja. Ale też regularne koszty. Jeśli chcesz pomóc w utrzymaniu i rozwoju strony, przekaż nam darowiznę w dowolnej wysokości







